Travelling Salesman Problem (TSP)
Notorious NP-hard problem and as such it does not have polynomial-time algorithms to find optimal solutions neither polynomial-time algorithm to verify such solution because the only way is to calculate it first.
Modelling the problem
- Cities are enumerated 0,1,2,3.. etc
- Adding points to a canvas
- The resulting TSP is then calculated and displayed
| Algorithm | Complexity | Description |
|---|---|---|
| Brute force | $ O(n!) $ | Try all permutation |
| Held Karp | $ O(n^22^n) $ | Dynamic programming |
| Heuristic Algorithm | ||
| Match Twice and Stitch | $ O(n^2) $ | Sequential matching |
| Lin–Kernighan heuristic | O(n⌊p1/2⌋) | Local search |
| Approximation | ||
| Nearest Neighbour | linear with approx factor log|V| | Greedy search |
| Christofides-Serdyukov | linear with approx factor 1,5 | MST |
| Double Tree | linear | MST |
Here there's two different approach to get some solutions.
2-Approximation Algorithm
Christofides' algorithm
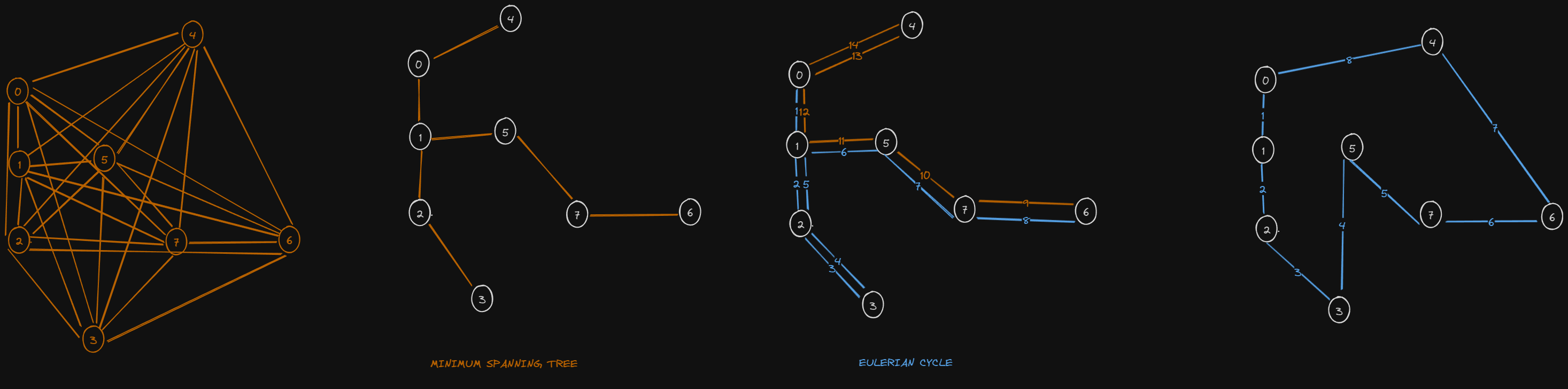
This approach is known as the Christofides' algorithm, which guarantees an approximation within a factor of 1.5 of the optimal solution. Here’s how the algorithm works:
- Construct the Minimum Spanning Tree (MST) of the graph.
- Find all vertices with an odd degree in the MST.
- Find a minimum-weight perfect matching for the odd-degree vertices.
- Add the edges of the matching to the MST, resulting in an Eulerian graph.
- Convert the Eulerian circuit to a Hamiltonian circuit by skipping repeated nodes, resulting in an approximate TSP solution.
This solution attept to solve
Traveling Salesman Problem (TSP), and it does so in a correct manner based on a widely-used heuristic known as theChristofides algorithm. While it doesn't always guarantee the optimal solution, it produces a good approximation in polynomial time.
- The
PrimMST.jscode calculates aMinimum Spanning Tree (MST), which ensures that all nodes are connected with the minimal total edge weight. The MST provides a lower bound for the TSP - The
EulerianPathFinder.jstakes the MST and transforms it into an Eulerian graph by doubling edges. Every node in an Eulerian graph has an even degree, allowing for the construction of anEulerian circuit(a path that visits every edge at least once). - The
geometricTSPfunction then "shortcuts" the Eulerian path by removing visits to already-visited nodes, taking advantage of the triangular inequality.
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| The draw is modelled as a Weighted Complete Graph | Calculate Minimum Spanning Tree (MST) | Each edge of MST is doubled producing an Eulerian Graph | The tour is the shortcutted |
| Each Node is a point in the cavas with (x,y) coordinates | MST calculated with Prim's Algorithm | An eulerian cycle that crosses every edge once is found | By the triangle inequality, the cost of the shortcut tour |
| The weights are the distance between the nodes | The graph distances are the lower bound for the TSP | is at most the cost of the Eulerian tour |
Self Organized Map
A self-organizing map (SOM) or self-organizing feature map (SOFM) is an unsupervised machine learning technique used to produce a low-dimensional (typically two-dimensional) representation of a higher-dimensional data set while preserving the topological structure of the data.
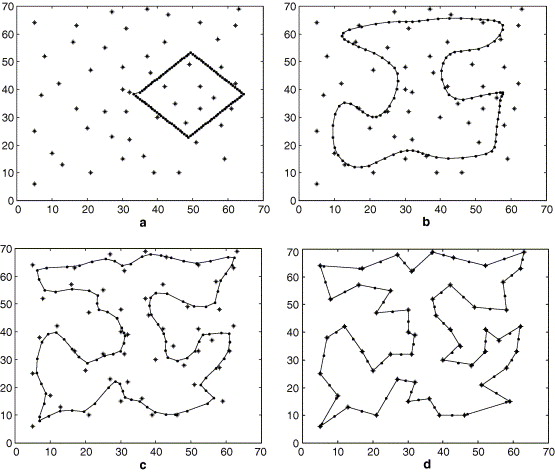
Travelling Salesman using Self Organized Maps
- you start with an arbitrary curve made up of many points
- each iteration you move the curve closer to the points inserting all the nodes
- the polygonal curve self adjust to fit all the points with the minimum distance.
Tensorflow js has been used as a tool to do operation with tensors directly on the browser client side.
Visual rapresentation