Methodology

1. Gray scale the image

A grayscale image is one in which the value of each pixel is a single sample representing only an amount of light


Linear Luminance	`let lightness = 0.2126 * pixels[i] + 0.715 * pixels[i+1] + 0.0722 * pixels[i+2];`	$Y = 0.2126 R + 0.7152 G + 0.0722 B $
Luma	`let lightness = parseInt(pixels[i].299 + pixels[i + 1].587 + pixels[i + 2]*.114);`	$Y = 0.299 R + 0.587 G + 0.114 B $
	`let lightness = parseInt(3pixels[i] + 4pixels[i + 1] + pixels[i + 2] >>> 3);`	$Y = 0.2627 R + 0.6780 G + 0.0593 B $

1. b Convert to a binary image using a threshold

const imageData = ctx.getImageData(0, 0, canvas.width, canvas.height);
const data = imageData.data;
 
// Convert to grayscale and detect edges
const grayscale = [];
const edges = [];
for (let y = 0; y < canvas.height; y++) {
    for (let x = 0; x < canvas.width; x++) {
        const i = (y * canvas.width + x) * 4;
        const r = data[i], g = data[i + 1], b = data[i + 2];
 
        // Simple grayscale conversion
        const gray = 0.3 * r + 0.59 * g + 0.11 * b;
        grayscale.push(gray);
 
        // Simple edge detection (using a threshold)
        if (gray < 240) {  // Threshold value to detect black borders (128 Default)
            edges.push({ x, y });
        }
    }
}

2. FloodFill

The algorithm looks for all nodes in the array that are connected to the start node by a path of the target color and changes them to the replacement color.

The algorithm use a stack (or queue) to prevent stack overflow that would happen with recursion.

Pseudocode

Flood-fill (node):
  1. Set Q to the empty queue or stack.
  2. Add node to the end of Q.
  3. While Q is not empty:
  4.   Set n equal to the first element of Q.
  5.   Remove first element from Q.
  6.   If n is Inside:
         Set the n
         Add the node to the west of n to the end of Q.
         Add the node to the east of n to the end of Q.
         Add the node to the north of n to the end of Q.
         Add the node to the south of n to the end of Q.
  7. Continue looping until Q is exhausted.
  8. Return.

2. Boundary tracing algorithm

Locate a boundary pixel: Start at a pixel known to be part of the border of the desired area.
Contour tracing: Begin tracing by moving to one of the neighboring pixels with the same color, following the boundary of the shape.
Moore-neighbor algorithm:

Move clockwise or counterclockwise, checking the 8 neighboring pixels, and follow the path formed by pixels of the same color.
If you reach a branch, continue following the border (since it is the same color).

Stop when you return to the starting pixel: Once you've fully traced the boundary.

Suzuki and Abe Algorithm (Topological Structural Analysis of Digitized Binary Images)
Best for: Binary images with multiple contours, including nested contours (like holes within objects).
How it works: It efficiently finds contours in binary images by following pixel chains. It's implemented in many image-processing libraries (like OpenCV) as cv.findContours.

4. Calculating the area

[Wiki] The shoelace formula, also known as Gauss's area formula and the surveyor's formula, is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their Cartesian coordinates in the plane. Trapezoid Formula

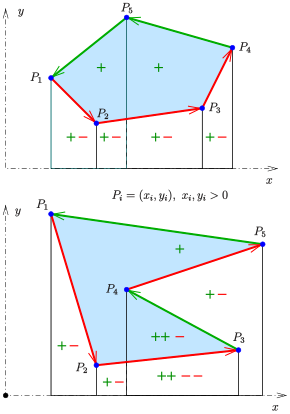
    function ShoelaceAlgorithm(){
        let sum = 0;
        for (let i = 0; i < n - 1; i++) {
            sum += (clicks[i + 1].x + clicks[i].x) * (clicks[i + 1].y - clicks[i].y)
        }
        sum += (clicks[0].x + clicks[n - 1].x) * (clicks[0].y - clicks[n - 1].y)
        return  Math.abs(sum / 2);
    }

5. Find point inside

CanvasRenderingContext2D.isPointInPath()

Ray casting algorithm

One simple way of finding whether the point is inside or outside a simple polygon is to test how many times a ray, starting from the point and going in any fixed direction, intersects the edges of the polygon. Wiki

    // Point-in-polygon algorithm (Ray-casting algorithm)
    function isPointInPolygon(x, y, polygon) {
        let isInside = false;
        const vertices = polygon.vertices;
        const n = vertices.length;
 
        for (let i = 0, j = n - 1; i < n; j = i++) {
            const xi = vertices[i].x, yi = vertices[i].y;
            const xj = vertices[j].x, yj = vertices[j].y;
 
            const intersect = ((yi > y) !== (yj > y)) &&
                              (x < (xj - xi) * (y - yi) / (yj - yi) + xi);
            if (intersect) isInside = !isInside;
        }
        return isInside;
    }

function point_in_polygon(point, polygon) {
    const num_vertices = polygon.length;
    const x = point.x;
    const y = point.y;
    let inside = false;
 
    let p1 = polygon[0];
    let p2;
 
    for (let i = 1; i <= num_vertices; i++) {
        p2 = polygon[i % num_vertices];
 
        if (y > Math.min(p1.y, p2.y)) {
            if (y <= Math.max(p1.y, p2.y)) {
                if (x <= Math.max(p1.x, p2.x)) {
                    const x_intersection = ((y - p1.y) * (p2.x - p1.x)) / (p2.y - p1.y) + p1.x;
 
                    if (p1.x === p2.x || x <= x_intersection) {
                        inside = !inside;
                    }
                }
            }
        }
 
        p1 = p2;
    }
 
    return inside;
}

References

[1] (Boundary tracing)(https://en.wikipedia.org/wiki/Boundary_tracing)
[2] (ContourTracing)(https://www.imageprocessingplace.com/downloads_V3/root_downloads/tutorials/contour_tracing_Abeer_George_Ghuneim/moore.html)
[3] (Point in polygon)(https://en.wikipedia.org/wiki/Point_in_polygon)
[4] (Shoelace formula)(https://en.wikipedia.org/wiki/Shoelace_formula)

Highlight a shape